Zenón fue un filósofo griego de la escuela eleática, nacido en Elea (Italia meridional). Fue discípulo de Parménides (uno de los filósofos griegos más importantes de la época y de los más señalados en la escuela eleática) y, según varios escritores, enseñó en Atenas durante algún tiempo.
Zenón trató de mostrar que la realidad es una e invariable y que todo movimiento es ilusorio.
Era costumbre suya mostrar lo absurdo de algunas creencias y frecuentemente se valía de paradojas (expresión o situación que parece absurda y sin embargo es razonable), en las que viene a decir que todo movimiento es un engaño.
Contrastadas con la realidad, las pruebas de Zenón contra el movimiento, se revelan al punto como paradojas y como auténticos paralogismos (argumento o contradicción falsa). Es como ponerse a discutir el azul del cielo.
Zenón, una gran influencia
El intento filosófico característico de Zenón es fundamentar la doctrina de su maestro Parménides de que no se da la pluralidad ni el movimiento, sino sólo un ser en reposo. Lo lleva a cabo con sus célebres cuatro argumentos contra el movimiento. Estos argumentos intrigaron profundamente a sus contemporáneos y a los pensadores posteriores.
Se tenía la impresión de que esos argumentos no podían ser válidos, pero resultaba muy difícil encontrarles los fallos, pues ni la ciencia lingüística, ni la lógica, ni la matemática habían alcanzado la madurez suficiente para ello. Pero el análisis de los argumentos dialécticos de Zenón, al igual que el de los más positivos de su maestro, sería una de las motivaciones que conducirían al posterior nacimiento de la lógica.
Los filósofos anteriores (milesios, pitagóricos, Heráklitos) habían presentado sus intuiciones y especulaciones de un modo directo, confiados en su aceptables ideas íntimas y esenciales.
Los eleáticos, Parménides y Zenón, fueron los primeros en argumentar, en ofrecer pruebas para explicar sus ideas y tesis. En Zenón, la argumentación se presenta tal y como él la ve, basada principalmente en la lógica y en la filosofía (por defectuosa que ésta fuera) y no por ello menos eficaz. El hecho de encontrar fallos en sus explicaciones o argumentos no es importante ya que no podemos olvidar que en Zenón encontramos, por primera vez, argumentaciones.
Entre sus argumentos más importantes destacan:
Argumento del estadio.- Un corredor no podrá recorrer una distancia concreta en toda su vida, ya que ésta se descompone en infinitos intervalos sucesivos de longitud, cada uno de los cuales ha de ser recorrido antes de recorrer el siguiente… y sin que nunca se llegue a recorrer el último, pues no lo hay (ya que la sucesión de intervalos es infinita)
Argumento de la flecha.- Similar al anterior.
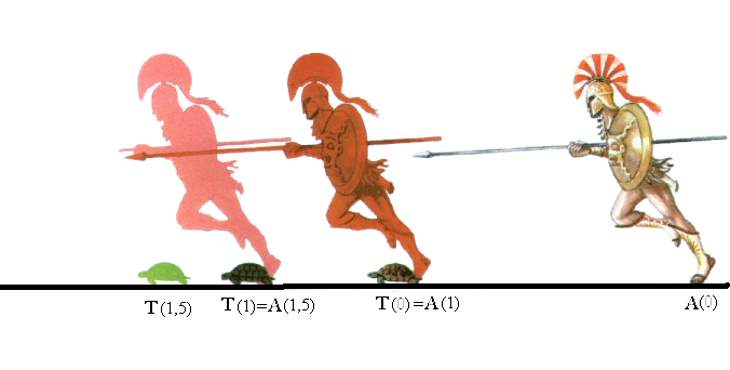
Argumento de Aquiles y la tortuga
Según este argumento, el más rápido de los hombres, Aquiles, no podrá alcanzar nunca al más lento de los animales, la tortuga, si se da a ésta una ventaja inicial en una carrera. Pues, mientras Aquiles recorre el camino que la tortuga llevaba por la mencionada ventaja inicial, la tortuga habrá recorrido otra porción, aunque más pequeña. Cuando Aquiles haya llegado a recorrer esta última porción de camino, la tortuga habrá avanzado otra porción más pequeña, y así la tortuga llevará siempre la ventaja hasta en espacios infinitamente pequeños, con lo cual, Aquiles no podrá alcanzarla nunca.

Se puede probar matemáticamente de «falsedad» del argumento de Aquiles. Veamos un razonamiento tomado de la página del profesor Bert Wachsmuth de la Universidad de Seton Hall en USA. Supongamos que la carrera tiene cien metros y Aquiles corre a una velocidad de 10 metros por segundo y la tortuga justo la mitad, es decir, 5 metros por segundo. La carrera se inicia con 10 metros de ventaja para la tortuga.
Si nos damos cuenta, al cabo de 2 segundos, Aquiles habrá recorrido 20 metros y la tortuga habrá recorrido 10 metros, es decir, ambos contendientes están situados en el punto correspondiente a los 20 metros, lo cual quiere decir que Aquiles ALCANZA a la tortuga y, por supuesto, gana la carrera, que ha terminado al cabo de 10 segundos al entrar Aquiles en la meta, mientras que la tortuga se encuentra en el punto correspondiente a los 60 metros en ese mismo momento.
Aquiles, llamado «el de los pies ligeros», decide salir a competir en una carrera contra una tortuga.
Ya que corre mucho más rápido que ella le da una ventaja inicial. Al salir, Aquiles recorre en poco tiempo la distancia que los separaba inicialmente, pero al llegar allí descubre que la tortuga ya no está, sino que ha avanzado, más lentamente, un pequeño trecho. Sin desanimarse, sigue corriendo, pero al llegar de nuevo donde estaba la tortuga, esta ha avanzado un poco más. De este modo, Aquiles no ganará la carrera, ya que la tortuga estará siempre por delante de él.
Aunque parezca lógico, es una paradoja porque la situación planteada contradice cualquier experiencia cotidiana: todo el mundo sabe que un corredor veloz alcanzará a uno lento aunque le dé ventaja.
Si supusiéramos (para simplificar) que Aquiles es solo diez veces más veloz que la tortuga y que la ventaja otorgada a esta última es de 10 metros, entonces, según argumenta Zenón, cuando Aquiles haya recorrido estos primeros 10 metros iniciales la tortuga ya estará más lejos (estará un metro más allá, es decir habrá recorrido un metro) y cuando Aquiles haya recorrido este nuevo metro para alcanzarla, la tortuga estará nuevamente más lejos (10 centímetros más). Aquiles continúa pero al llegar allí, la tortuga estará otro centímetro más lejos (es decir en los 11 metros y 11 centímetros) así sucesivamente.
Desde el punto de vista matemático, el concepto que subyace a la paradoja es el de serie, más precisamente, la existencia de las series convergentes. Lo que aplica a la situación que plantea la paradoja es que la suma de infinitos términos puede ser finita.
Si se suman los segmentos recorridos por Aquiles se obtiene una serie geométrica convergente:
Lo aclararemos estudiando como sucesiones las distancias recorridas, la ventaja de la tortuga y los tiempos empleados:
|
Posición de Aquiles (m.) |
Posición de la tortuga (m.) |
Ventaja de la tortuga (m.) |
Tiempo empleado (seg.) |
|
| Salida
1ª etapa 2ª etapa 3ª etapa 4ª etapa … Límites |
0
100 100 + 10 = 110 100 + 10 + 1 = 111 100 + 10 + 1 + 0,1 = 111,1 … 111,111… |
100
100 + 10 = 110 100 + 10 + 1 = 111 100 + 10 + 1 + 0,1 = 111,1 100 + 10 + 1 + 0,1 + 0,01 = 111,11 … 111,111… |
100
10 1 0,1 0,01 … 0 |
0
10 10 + 1 = 11 10 + 1 + 0,1 = 11,1 10 + 1 + 0,1 + 0,01 = 11,11 … 11,111… |
Así, en la interpretación moderna, basada en el cálculo infinitesimal que era desconocido en época de Zenón, se puede demostrar que Aquiles realmente alcanzará a la tortuga, sobre la base de la demostración del matemático escocés James Gregory (1638-1675) acerca de que una suma de infinitos términos puede tener un resultado finito.
Los tiempos en los que Aquiles recorre la distancia que lo separa del punto anterior en el que se encontraba la tortuga son cada vez más y más pequeños (hasta el infinito más pequeños), y su suma da un resultado finito, que es el momento en que alcanzará a la tortuga.
Otra manera de plantearlo es que Aquiles puede fijar un punto de llegada que está metros delante de la tortuga en vez del punto en que ella se encuentra. Ahora, en vez de cantidades infinitas, tenemos dos cantidades finitas con las cuales se puede calcular un intervalo finito de tiempo en el cual Aquiles pasará a la tortuga.
También se puede encarar el problema evitando el cálculo infinitesimal, cuyo planteamiento matemático se desconocía en tal época, para reconvertirlo en análisis discreto: Filípides—el campeón olímpico al que se ordenó que abandonara las filas del ejército para comunicar a Atenas la victoria conseguida sobre los persas en la playa de Maratón— no recorre espacios infinitesimales, sino discretos, que podemos denominar zancada.
A cada zancada le podemos asignar un espacio concreto.
Por ejemplo podemos suponer que Filípides recorre un metro a cada zancada. Ahora el problema se reduce a la comparación de velocidades relativas: calcular en qué momento la última zancada de Filípides recorrerá una distancia mayor a la que haya podido recorrer la tortuga en el mismo tiempo, incluso aunque no sepamos definir la distancia exacta que la tortuga recorrería. Es decir, basta que una de las variables sea discreta y que podamos suponer que, en determinado tiempo, puede superar a las distancias infinitesimales, para demostrar, incluso teóricamente, que el movimiento existe.
Existe además otra variante para describir la paradoja, según la cual Aquiles nunca podría partir siquiera. Así planteada la aporía, se sostiene que Aquiles, antes de que pueda recorrer el tramo que dio en ventaja a la tortuga tendría que haber ya recorrido la mitad de ese trecho y antes de él, haber superado ya un cuarto, previamente un octavo y antes de eso un dieciseisavo y así sucesivamente, de modo que nunca podría ponerse en marcha.
Lo que sí es seguro que la solución no puede salir de una argumentación distinta a la original, sino del estudio del enunciado original, lugar en el que se encuentra el error, mal entendido, o paradoja.





Deja una respuesta